Understanding Factorials: Exploring the Concept and Calculation Methods

Introduction to Factorials

Factorials are a fundamental concept in mathematics and play a significant role in various fields, including combinatorics, probability theory, and computer science. Understanding factorials is crucial for solving problems involving permutations, combinations, and recursive algorithms. In this article, we will delve into the concept of factorials, explore their properties, and discuss different methods to calculate them.

What is a Factorial?

Definition of a Factorial

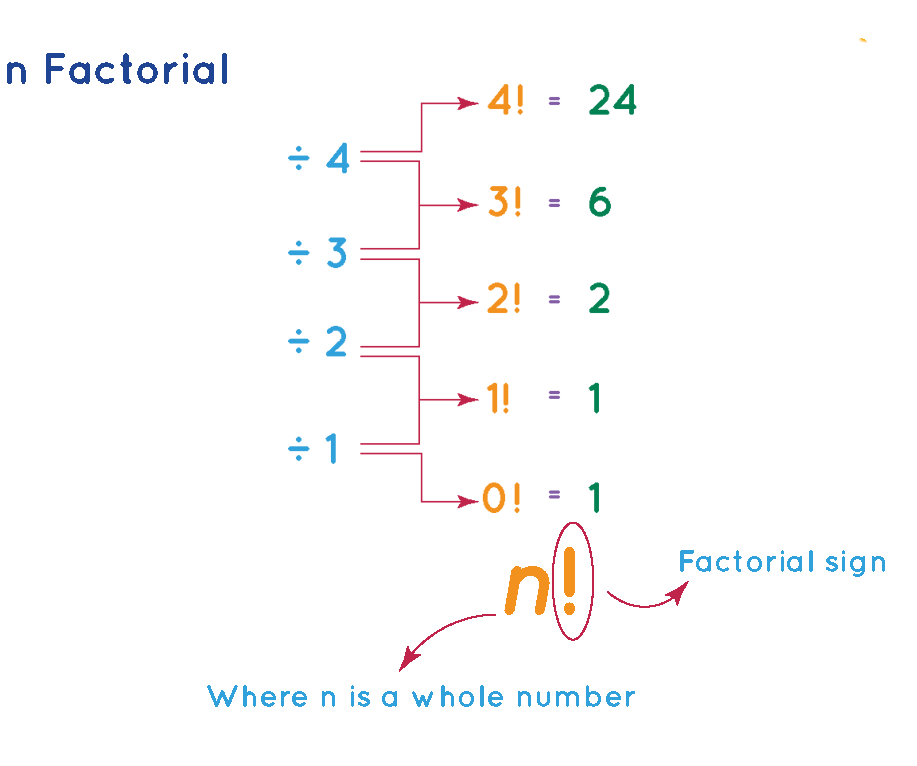
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers from 1 to n. It can be expressed as:

scssCopy coden! = n * (n-1) * (n-2) * ... * 3 * 2 * 1

For example, 5! (read as “5 factorial”) is calculated as:

Copy code5! = 5 * 4 * 3 * 2 * 1 = 120

Properties of Factorials

Property 1: 0! and 1!

The factorial of 0, denoted as 0!, is defined to be 1. Similarly, the factorial of 1, denoted as 1!, is also 1. These base cases are essential for recursive calculations and help maintain consistency in factorial operations.

Property 2: Factorial of Negative Integers

Factorials are not defined for negative integers. The factorial operation is restricted to non-negative integers because it represents the concept of counting objects or arranging elements.

Property 3: Factorial of Large Integers

Factorial calculations can result in very large numbers, especially for large values of n. The growth of factorials is exponential, which means the result grows rapidly as n increases. This exponential growth poses practical limitations when working with factorials, especially in terms of memory and computation time.

Methods to Calculate Factorials

Method 1: Iterative Approach

The iterative approach involves using a loop to calculate the factorial step by step. Starting from 1, each iteration multiplies the current value by the next integer until n is reached.

Method 2: Recursive Approach

The recursive approach uses a function that calls itself to calculate the factorial. The base case is when n equals 0 or 1, in which case the function returns 1. For other values of n, the function recursively calls itself with n-1 as the argument and multiplies the result by n.

Method 3: Mathematical Formula

For certain values of n, there exist mathematical formulas to directly calculate the factorial. These formulas leverage mathematical properties and patterns to simplify the computation. One such example is Stirling’s approximation, which provides an approximation of factorials for large values of n.

Practical Applications of Factorials

Factorials find applications in various domains, including:

• Combinatorics: Factorials are used to calculate permutations and combinations, which are essential in probability theory, statistics, and counting problems.
• Recursive Algorithms: Many recursive algorithms, such as those involving tree structures or backtracking, rely on factorials for calculating the number of possible outcomes.
• Probability and Statistics: Factorials are used in determining the number of possible outcomes in sample spaces and calculating probabilities.
• Cryptography: Factorials are used in cryptographic algorithms for key generation and security protocols.

Conclusion

Factorials are a powerful mathematical concept with